Dynamical Systems for Motion Learning

This page introduces multiple projects where dynamical systems are shaped using imitation learning to model robot motions. Various inductive biases are designed and incorporated into these systems based on prior knowledge of their behavior. The exploration and exploitation of systems with a single global attractor, multiple attractors, region avoidance, evolution in non-Euclidean geometries, and cyclical behaviors are examined in the context of robotics.

1. Reaching Tasks

1.1. CONDOR

This work merges dynamical systems with deep neural networks, ensuring that the robot’s goal state is a globally asymptotically stable equilibrium within the learned dynamical system. This provides a robust inductive bias for reaching tasks. We achieved this by introducing a novel loss function, drawing on concepts from the deep metric learning literature to enhance the stability and reliability of robotic movements.

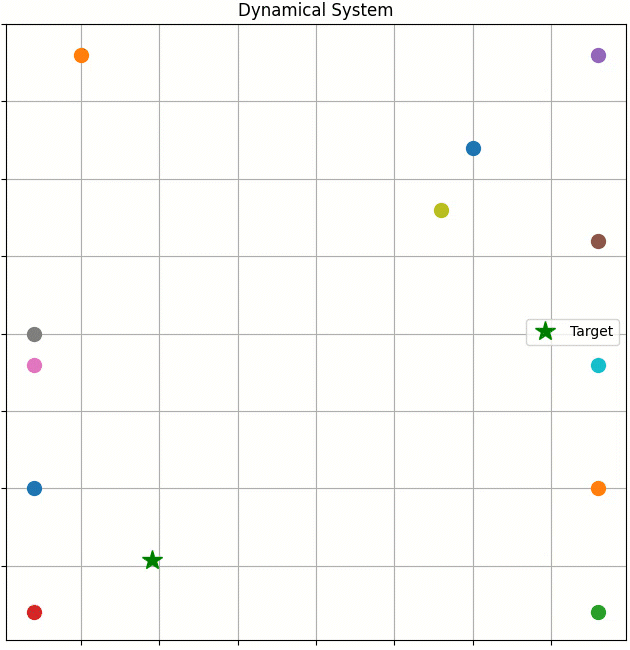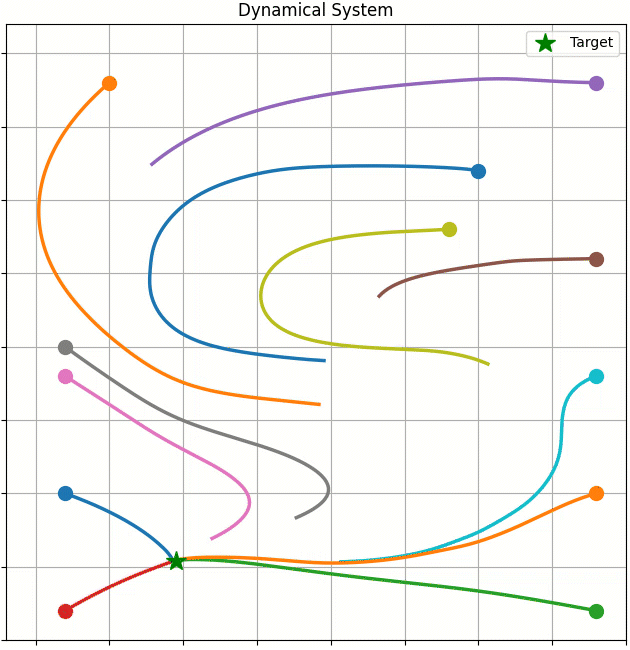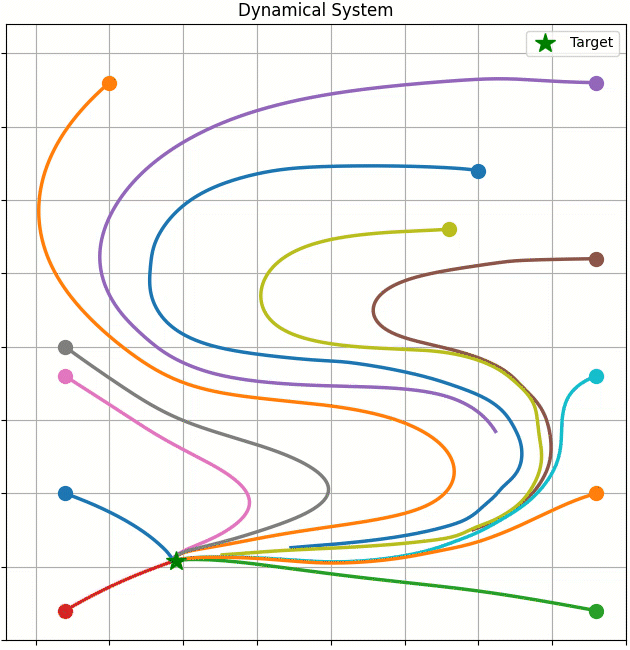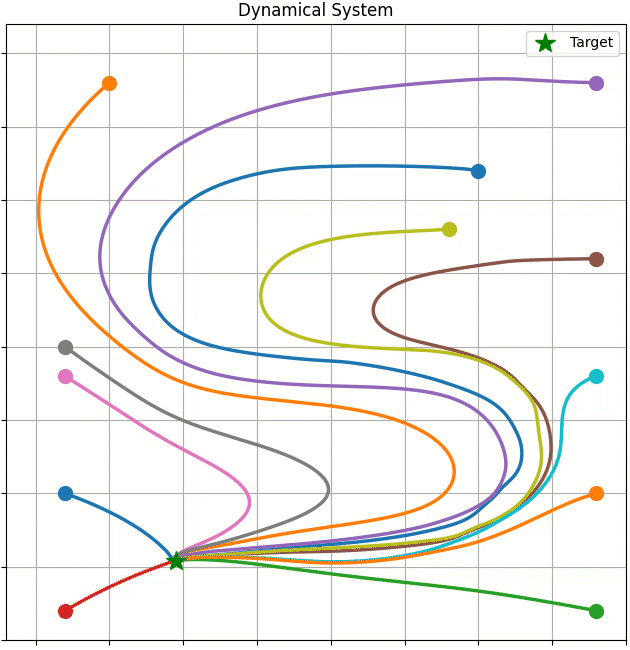
Paper:

@article{PerezDattari2023TRO,
  author  = {P\'{e}rez-Dattari, Rodrigo AND Kober, Jens},
  journal = {IEEE Transactions on Robotics},
  title   = {Stable Motion Primitives via Imitation and Contrastive Learning},
  year    = {2023},
  pages   = {1--20},
  doi     = {10.1109/TRO.2023.3289597},
  code    = {https://github.com/rperezdattari/Stable-Motion-Primitives-via-Imitation-and-Contrastive-Learning},
  file    = {https://arxiv.org/pdf/2302.10017.pdf},
}
      

Links:

Project members:
R. Pérez-Dattari and J. Kober
2023

1.2. PUMA

This project builds upon some of the ideas developed with CONDOR and addresses its limitations while providing a simpler framework. In particular, it enables easy learning of dynamical systems in non-Euclidean geometries, which are essential for problems that require orientation control. Additionally, it demonstrates improved performance in learning second-order dynamical systems.

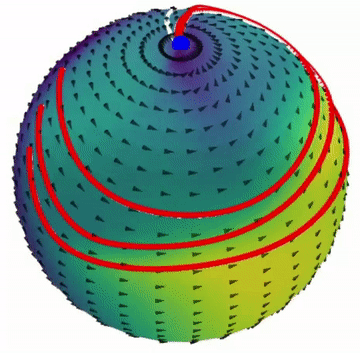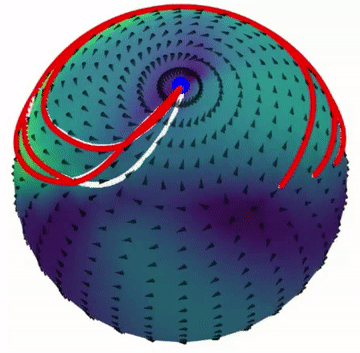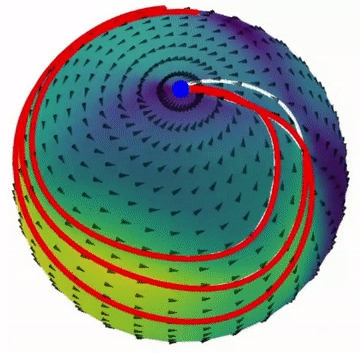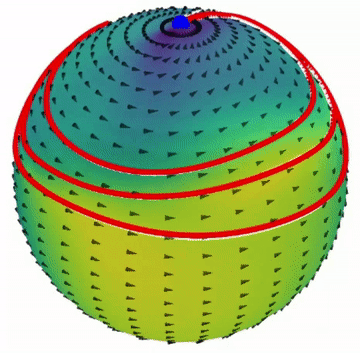
Paper:

@article{PerezDattari2024AISY,
  author  = {P\'{e}rez-Dattari, Rodrigo AND Della Santina, Cosimo AND Kober, Jens},
  journal = {Advanced Intelligent Systems},
  title   = {PUMA: Deep Metric Imitation Learning for Stable Motion Primitives},
  year    = {2024},
  note    = {Accepted},
}
      

Links:

Project members:
R. Pérez-Dattari, C. Della Santina and J. Kober
2024

2. Geometry-Aware Reaching Tasks

This work introduces TamedPUMA, a framework that combines the strengths of Geometric Fabrics and PUMA. Specifically, PUMA’s ability to learn globally asymptotically stable motions is integrated with Geometric Fabrics’ capability to safely merge dynamical systems operating in multiple task spaces, enabling features such as whole-body obstacle avoidance while following learned behaviors.

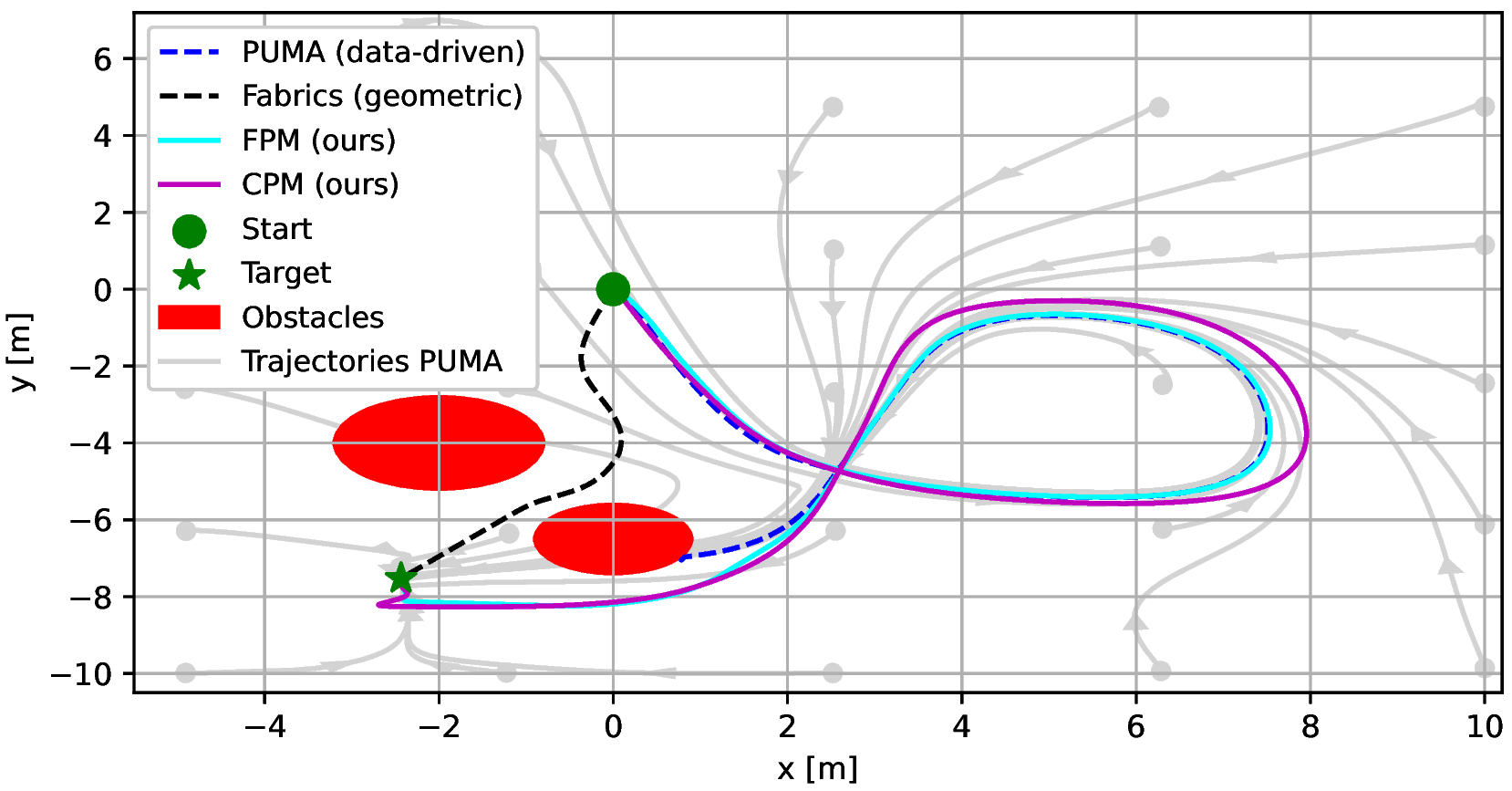
x1

Paper (workshop):

@misc{bakkersafe2024,
  title={Safe and stable motion primitives via imitation learning and geometric fabrics},
  author={Bakker, Saray and P{\'e}rez-Dattari, Rodrigo and Della Santina, Cosimo and B{\"o}hmer, Wendelin and Alonso-Mora, Javier},
  year={2024},
  howpublished={Presented at the 20th Robotics: Science and Systems (RSS) Workshop, Priors4Robots},
}
      

Links:

Project members:
S. Bakker, R. Pérez-Dattari, C. Della Santina, W. Bohmer and J. Alonso-Mora
ongoing

3. Multi-Objective Reaching Tasks

In this project, we address problems where reaching multiple goal states is equally desirable, rather than having a single goal state. We model this using multi-attractor dynamical systems, with stability enforced by a novel method that extends PUMA.

x1

x1

Project members:
G. Di Marzo, R. Pérez-Dattari, M. Stölzle, M. Ramirez-Montero and C. Della Santina
ongoing

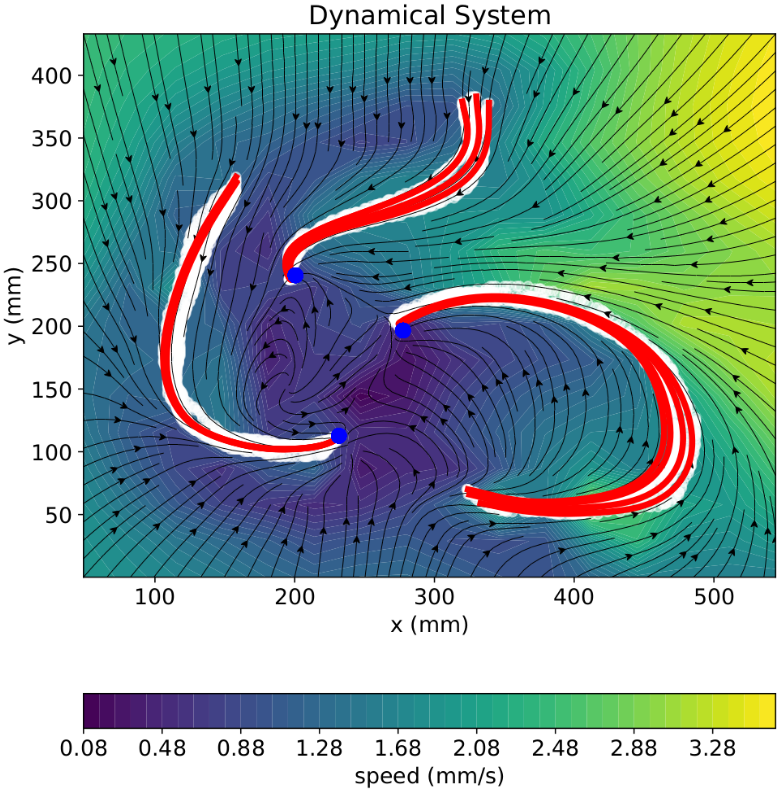
4. Cyclic Tasks

This work leverages invertible neural networks to enforce dynamical systems to contain a limit cycle, with its shape derived from demonstrations. This approach is particularly useful for cyclic tasks, such as cleaning, walking, or swimming.

x5

x1

Project members:
M. Stölzle, T. Konstantin Rusch, Z. J. Patterson, R. Pérez-Dattari, F. Stella, J. Hughes, C. Della Santina and D. Rus
ongoing